어떤 연속되는 특정 구간 쿼리를 처리하기 위해서 원소들의 각 구간을 √N개로 분할하여 관리하는 알고리즘이다.
원소의 개수가 N, 쿼리의 개수 M이라고 한다면
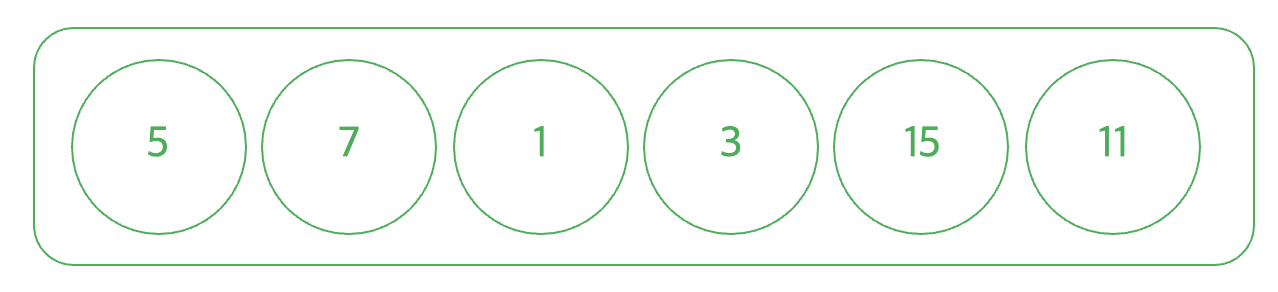
만약 선형 탐색을 한다면 각 구간 별로 최악의 경우 N번을 확인해야 하기 때문에 쿼리의 수를 곱한 시간 복잡도는 O(MN)이 걸리게 된다.
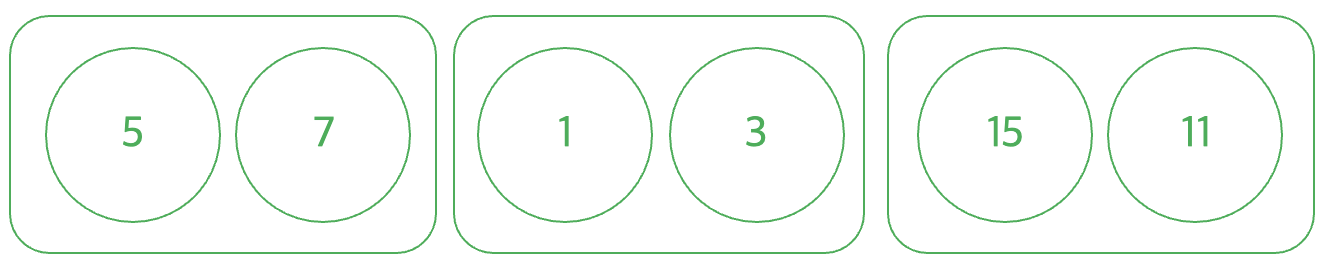
해당 알고리즘을 이용하면 구간별로 미리 나누어 구해놓았기 때문에 전부 확인할 때 √N의 연산만이 필요하다. 하지만 항상 구간에 맞아떨어지는 건 아니기 때문에 추가로 걸쳐있는 구간을 구하는 연산도 필요하다.
시간복잡도는 완전히 포함하는 구간 M√N, 구간에 걸쳐있는 부분은 커봐야 2√N보다 작은 숫자이므로 O(M√N)이 된다.
구현
구간합 소스를 예제로 구현해보자
문제 링크 : 2042_구간 합 구하기
초기화(init)
각 구간을 √N으로 나누어서 bucket(각 구간별 총합)을 미리 구한다.
arr = [int(input()) for _ in range(N)]
bucket = [0] * (N // int(N ** .5) + 1)
section = int(N ** .5)
def init():
for i in range(N):
bucket[i // section] += arr[i]
값 변경(update)
값이 변경이 일어나면 해당 bucket의 총합에 기존 값을 빼고 바뀐 값으로 더해주고 arr 배열 상태를 변경된 상태로 변경해준다.
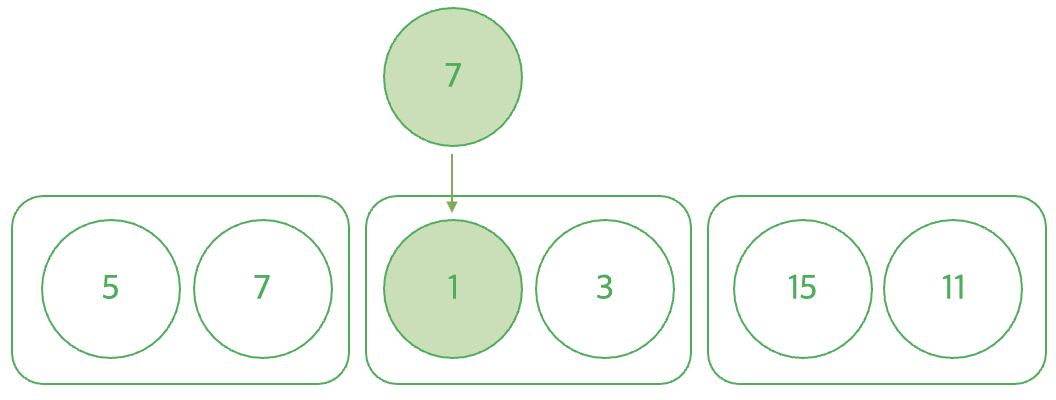
def update(idx, value):
bucketIdx = idx // section
bucket[bucketIdx] -= arr[idx]
bucket[bucketIdx] += value
arr[idx] = value
구간합 구하기
좌우 해당하는 버킷이 같다면 해당 범위에 있는 인덱스만 더해 반환하면 되고 그렇지 않다면 좌우 걸치는 공간을 더해주고 완전히 포함하는 버킷을 더해준다.

def getSum(s, e):
ret = 0
l, r = s // section, e // section
# 같은 버킷에 존재한다면
if l == r:
for i in range(s, e + 1):
ret += arr[i]
return ret
# 걸쳐있는 부분 더하기
while s // section == l:
ret += arr[s]
s += 1
while e // section == r:
ret += arr[e]
e -= 1
# 완전히 포함된 버킷 더하기
for i in range(s // section, e // section + 1):
ret += bucket[i]
return ret
전체 소스
input = __import__('sys').stdin.readline
def init():
for i in range(N):
bucket[i // section] += arr[i]
def update(idx, value):
bucketIdx = idx // section
bucket[bucketIdx] -= arr[idx]
bucket[bucketIdx] += value
arr[idx] = value
def getSum(s, e):
ret = 0
l, r = s // section, e // section
if l == r:
for i in range(s, e + 1):
ret += arr[i]
return ret
while s // section == l:
ret += arr[s]
s += 1
while e // section == r:
ret += arr[e]
e -= 1
for i in range(s // section, e // section + 1):
ret += bucket[i]
return ret
if __name__ == '__main__':
N, M, K = map(int, input().split())
arr = [int(input()) for _ in range(N)]
bucket = [0] * (N // int(N ** .5) + 1)
section = int(N ** .5)
init()
for _ in range(M + K):
op, *elements = map(int, input().split())
if op == 1:
update(elements[0] - 1, elements[1])
else:
print(getSum(elements[0] - 1, elements[1] - 1))