사전 지식
오프라인 쿼리(Offline Query)
어려운 개념은 아니고 쿼리(입력)가 들어오면 바로 처리하는 것이 아니라 데이터를 다 입력받고 필요에 배열을 재배치하여 좀 더 효율적으로 접근하는 방식을 말한다.
평방 분할(Sqrt Decomposition)
연속된 데이터의 집합을 √N의 구간으로 나누어 미리 값을 구해놓고 데이터를 처리하는 것을 말한다.
자세한 설명 : 바로가기
모스 알고리즘(Mo’s Algorithm)
모스 알고리즘은 투 포인터와 닮아있다. 입력으로 받은 쿼리를 재배치(오프라인 쿼리)하는데 재배치할 때 기준은 평방 분할을 이용하고 투 포인터를 이용해 현재 쿼리에서 다음 쿼리까지 오차가 있는 양 끝점을 조금씩 이동해주면 된다.
투 포인터 + 오프라인 쿼리 + 평방 분할 짬뽕이라고 생각한다.
일단 이 알고리즘을 쓰기 위해서는 update 연산이 없어야 한다. 왜냐하면 쿼리를 내 맘대로 재배치할 것이기 때문이다. 쿼리를 재배치할 때 기준은 [s, e] 구간 쿼리가 있을 때 왼쪽을 기준으로 sqrt(s)한 결과 값으로 오름차순, 그리고 왼쪽 값이 같을 때 오른쪽 구간도 오름차순 해주면 된다.
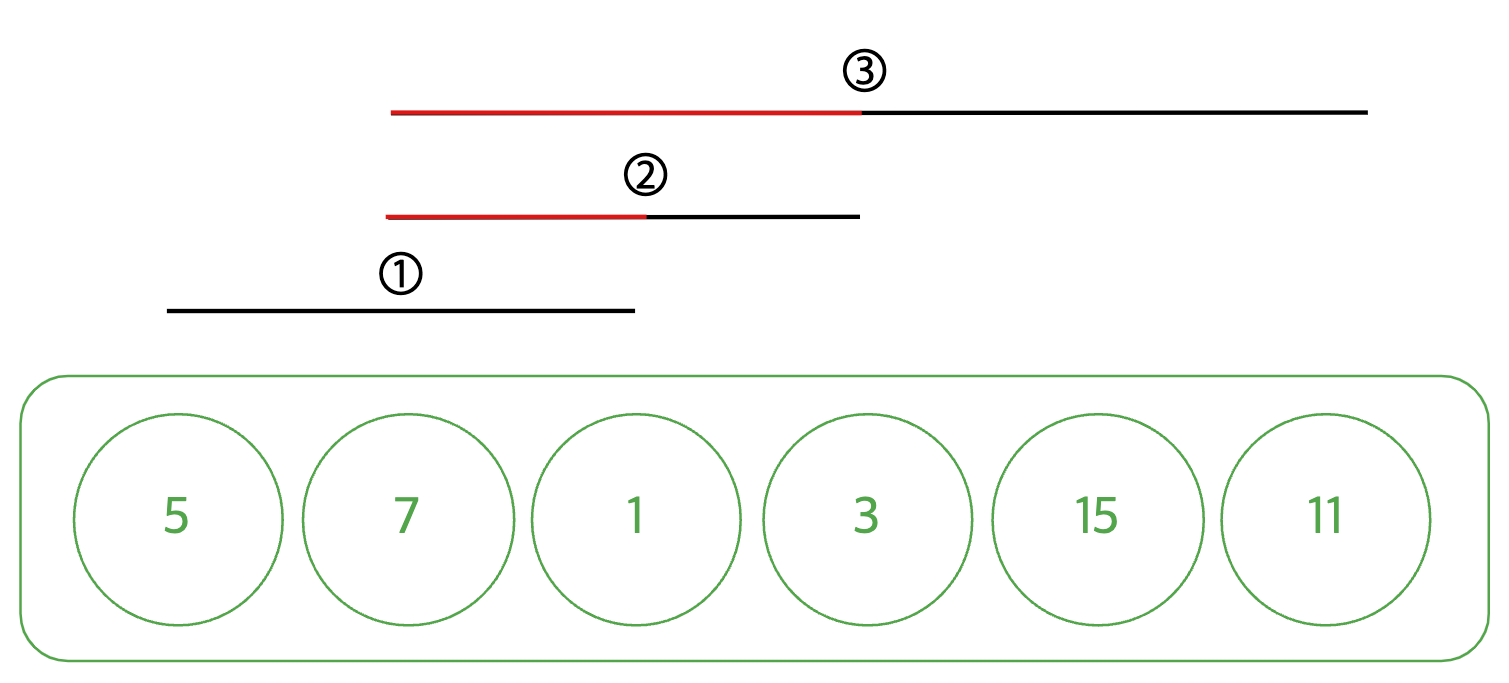
위 사진을 보면 배열이 있고 검은색 선(세 개의 쿼리)이 정렬되어있는 사진이다. 빨간색으로 색칠된 부분은 이미 이전에 계산해놓은 값을 가져다가 쓰기 때문에 따로 계산해 줄 필요가 없으므로 이러한 이점을 이용해서 푸는 알고리즘이다.
시간 복잡도는 O((Q + N)√N)이다.
- 왼쪽 이동 : Q(쿼리의 개수) * √N(sqrt로 나눈 구간 내에서 이동 가능)
- 오른쪽 이동 : N(오름차순으로 정렬했고 배열의 크기만큼 이동 가능) * √N(sqrt로 나눈 각 구간만큼)
구현
구간합과 비슷한 문제를 예제로 구현해보자
문제 링크 : 8462_배열의 힘
문제 설명
자연수로 이루어진 배열이 주어지고 부분 배열의 힘이라는 것을 구한다. 이때 힘은 부분 배열에 있는 자연수 * 해당 자연수의 빈도 수 ** 2를 존재하는 자연수 모두 더해주면 된다.
이 문제는 update 연산이 없으므로 쿼리 순서를 마음대로 바꿀 수 있고 사실 구하는 방법만 다르지 구간합과 다를 것 없다.
쿼리 재배치
쿼리를 받고 이 쿼리가 몇 번 째 답인지 알아야 하므로 index만 뒤에 붙여서 저장하고 왼쪽 기준으로 sqrt한 값과 오른쪽 값으로 오름차순으로 정렬한다.
cnt = [0] * 1000001 # 각 숫자 빈도수
ans = [0] * T # 정답 담을 배열
res = 0 # 현재 힘
for i in range(T):
s, e = map(int, input().split())
query.append((s, e, i))
query.sort(key=lambda x: (int(x[0] ** .5), x[1]))
다음 쿼리로 이동
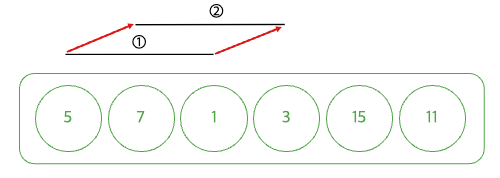
아까 투 포인터와 닮았다고 말했고 현재 쿼리 구간을 다음 쿼리 구간으로 왼쪽, 오른쪽 포인터 지점을 변경시켜주는 것이 필요하다. 이때 움직일 때마다 힘을 바로 계산해주면 된다. 이렇게 해주지 않으면 나중에 힘을 계산할 때 존재할 수 있는 자연수의 배열을 linear search 해야 하기 때문이다.
def insert(val):
global res
res -= cnt[val] ** 2 * val
cnt[val] += 1
res += cnt[val] ** 2 * val
def delete(val):
global res
res -= cnt[val] ** 2 * val
cnt[val] -= 1
res += cnt[val] ** 2 * val
def move(ss, se, es, ee):
for i in range(ss, es):
delete(arr[i])
for i in range(se, ee, -1):
delete(arr[i])
for i in range(ss - 1, es - 1, -1):
insert(arr[i])
for i in range(se + 1, ee + 1):
insert(arr[i])
전체 소스
input = __import__('sys').stdin.readline
def insert(val):
global res
res -= cnt[val] ** 2 * val
cnt[val] += 1
res += cnt[val] ** 2 * val
def delete(val):
global res
res -= cnt[val] ** 2 * val
cnt[val] -= 1
res += cnt[val] ** 2 * val
def move(ss, se, es, ee):
for i in range(ss, es):
delete(arr[i])
for i in range(se, ee, -1):
delete(arr[i])
for i in range(ss - 1, es - 1, -1):
insert(arr[i])
for i in range(se + 1, ee + 1):
insert(arr[i])
if __name__ == '__main__':
N, T = map(int, input().split())
arr = [0] + list(map(int, input().split()))
query = []
cnt = [0] * 1000001
ans = [0] * T
res = 0
for i in range(T):
s, e = map(int, input().split())
query.append((s, e, i))
query.sort(key=lambda x: (int(x[0] ** .5), x[1]))
l = r = query[0][0]
r -= 1
for i in range(T):
s, e, idx = query[i]
move(l, r, s, e)
l, r = s, e
ans[idx] = res
for i in ans:
print(i)